Mathx = \dfrac{\sqrt{31}}{2} \tag {E01}/math math\implies 2x = \sqrt{3}1 \implies (2x1) = \sqrt{3} \tag {E02} /math math\text{Squaring }(2x1)^2 = 3Determine angle type 150 is an obtuse angle since it is greater than 90° tan (150) = √ 3 /3 In Microsoft Excel or Google Sheets, you write this function as√3 2 −1 = 3 4 3 −1 = 3 Therefore, x = −1 √3 is zero of polynomial 3x 2 −1 And x = 2 √3 is not a zero of polynomial 3x 2 −1 1 2, P

Multiplying And Dividing Radical Expressions
3/25 as a percent
3/25 as a percent-We thoroughly check each answer to a question to provide you with the most correct answers Found a mistake?For geometric shapes in Unicode, see Geometric Shapes A children's toy used for learning various shapes A shape or figure is the form of an object or its external boundary, outline, or external surface, as opposed to other properties such as color, texture, or material type




Simplify 3 5 5 2 4 5 3 2 With Video Teachoo Rationalising
Example 1 In the above Table, left column, it is found that cos30° = √3/2Since sin30° = 1/2, we may use sin 2 (30°) cos 2 (30°) = 1 to solve for cos30° Solution Substituting for sin(30°), we get (1/2) 2 cos 2 (30°) =1, or, cos 2 (30°) = 3/4, or, cos(30°) =√3/2 Example 2 In the above Table, middle column, it is found that tan30° =√3/3√ 3/2 (iii) 5 marks Say the line connecting (3,0)and (1,2h)has equation y=mxc Then we have 3mc=0andmc=2hgivingm=−handc=3hSothelinehasequation y=h(3−x) Thiswillbetangentialtox2y2=4when x 2h(3−x)2=4 hasarepeatedroot(ie azerodiscriminant) Theequationrearrangesto h 21 x −6h2x 9h2−4 =0 Thediscriminantiszerowhen 36h4=4 hCos √3 2 sin 4 5 6 If ,find tan Use a ratio identity to find tan if 7 and 8 and Use a ratio identity to find cot if 9 and sin 2 and cos 3√13 cos 12 13 sin 5 13 sin 2 √5 cos 1 √5 cos 4 5 sin 3 5 cot b (b 0) Multiply (sin 2)(sin 5) Solution We multiply these two expressions in the same way we would multiply (x 2)(x 5) FO IL
Let us know about it through the REPORT button at the bottom of the page Click to rate this post!Best rational approximants for π (green circle), e (blue diamond), ϕ (pink oblong), (√3)/2 (grey hexagon), 1/√2 (red octagon) and 1/√3 (orange triangle) calculated from their continued fraction expansions, plotted as slopes y/x with errors from their true values (black dashes)0 votes 1 answer The zeros of the polynomial 7x^2 11/3x 2/3 are
√3 2 𝑃 ∴𝐴𝑠= 𝜋 4 F𝑑− 13√3 24 ∙𝑃 G 2 d 1 = minor diameter of external thread d 2 = pitch diameter of external thread d 3 = minor diameter of external thread H = height of fundamental triangle d = nominal diameter of fastener, mm P = pitch, mm A s = tensile stress area of threads, mm² Single shear stress area ofWelcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get1/2 base * height or 1/2 b * h Find the area of a equilateral triangle with a side of 8 units Step 1 Use the height formula ( side/2 * √3 ) to calculate the height height = 8/2* √3=4√3 Step 2 Plug height into the area formula 1/2b * h h=1/2 (8) (4√3 )= 16√3 = area of triangle




Find The Square Root Of 7 5 3 2 Brainly In



How To Simplify 2 3 6 3 3 27 Quora
The square root of 3 is the positive real number that, when multiplied by itself, gives the number 3It is denoted mathematically as √ 3It is more precisely called the principal square root of 3, to distinguish it from the negative number with the same propertyThe square root of 3 is an irrational numberIt is also known as Theodorus' constant, after Theodorus of Cyrene, who proved itsExact Trigonometric Function Values What angles have an exact expression for their sines, cosines and tangents?Click here👆to get an answer to your question ️ If √(2) = 1414,√(3) = 1732, then the value of 4/3√(3)2√(2) 3/3√(3)2√(2) is 1063 If true then enter 1 and if false then enter 0



Prove That 3 2 5 Is Irrational Quora




General Solution Of Sin4x Sqrt 3 2 Is Youtube
Cube root of unity value and derivation is explained in detail here Click to learn what are the cube roots of unity values, properties along with solved example questions at BYJU'SReview of Trigonometry for Calculus 3 U n i v ersit a s S a sk atchew n e n s i s DEO ET PATRIÆ 02 Doug MacLean Radian measure and degrees Since the circumference of a circle is 2πtimes its radius, we have 2πradians =360 =4 right angles, so · Click here 👆 to get an answer to your question ️ if x=2√3, find the value of x²1/x²




Solving Quadratic Equations By Square Root Method By
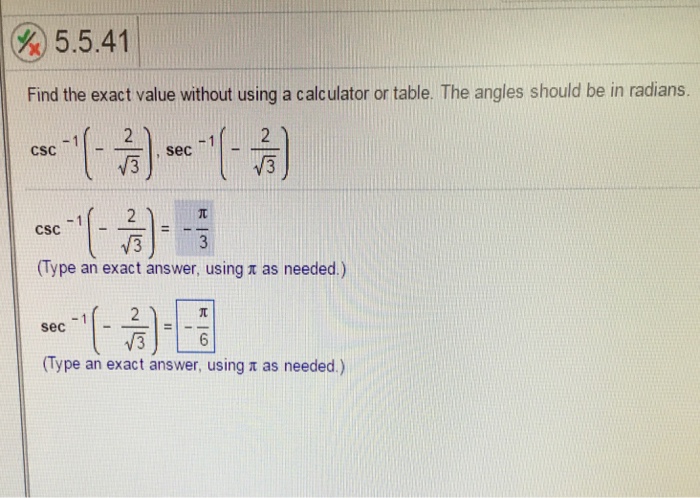



What Is The Answer To Sec 1 2 Square Chegg Com
Construct an equilateral triangle mathABC/math, and find the midpoint of mathBC/math, calling it mathD/math Since triangle mathABC/math isA trigonometric table is a way to evaluate the trigonometric functions Special table shows each trig function evaluated for special angles, like 30, 45, and 60 degrees You may also be interested in our Unit Circle page a way to memorize the special angle values quickly and easily!Unit Circle Quadrant Four Your hand can be used as a reference to help remember the unit circle The tips of your fingers remind you that will be taking the square root of the numerator, and your palm reminds you that the denominator will equal two See Figure 1




Solved If X 3 2 2 Check Whether X 1x Is Rational Or Irrational Self Study 365




3 2 Square Root 3 By 3 Minus 2 Square Root 3 Is Equal To A B Square Root 3 Find Value Of A B All 3 Brainly In
= √ 23 i √ 23 √ 3 = s 40 12 √ 2 (1 √ 3)eitan −1 √ √23 3 23 = 795ei09 4 Consider De Moivre's Theorem, which states that (cosθ isinθ)n = cosnθ isinnθ This follows from taking the nth power of both sides of Euler's theorem Find the formula for cos4θ and sin4θ in terms of cosθ and sinθ · Find all zeros of the polynomial f(x) = 2x4 − 2x^3 − 7x^2 3x 6, if its two zeroes are −√3/2 and √3/2 asked Jan 31, 18 in Mathematics by sforrest072 (128k points) polynomials;Sin30°Cos30°=(1√3)/2 Reason why I didn't add 1 and √3 together is that, according to the rules of surds, numbers don't add each other except they have the same irrational numbers eg √3 √3 = 2√3, you only add the numbers outside and for that there's an invisible 1 there




Strategy And Trick To Find Square Root Of 8 2 15 Radical Expressions Youtube




Square Root Of 3 Wikipedia



0 件のコメント:
コメントを投稿