分配法則 分配法則とは、下のような（ ）をはずす計算ルールのことです。 a(bc) = ab ac a ( b c) = a b a c a(b−c) = ab− ac a ( b − c) = a b − a c ※ a,b,c a, b, c が負の数であったり、 b,c b, c の大小関係次第でこの図は万能ではありません。 イメージがついてもらえればOKです。 要は、スラスラ計算できるようになることが重要です。分配法則 (練習問題) かけ算の性質 カーンアカデミー かけ算の項を分解する練習問題をして，それが積にどのように影響するかみてみましょう。 かけ算の項を分解する練習問題をして，それが積にどのように影響するかみてみましょう。 If you're seeing this message, it means we're having trouble loading external resources on our websiteはじめに 計算をすることは、数学の宿命です。逃げられません！ 内容が難しくなるにつれて、計算も複雑になってきます・・・ 二つの「楽」 ラクしてタノシク問題に取り組むために必要となってくるのが、「分配法則」です。 分配法則とは 分配法則とは、計算
ベスト中2 数学 式の計算 問題 最高のぬりえ
中1 数学 分配法則 問題
中1 数学 分配法則 問題- まずは 分配法則 からです。 今までの分配法則は2(x5)みたいなやつ。 これからの分配法則は2x(x3)=2x 2 6xのように2乗が出てきたり、(x3a)(a8b)みたいに()が続いたりします。 解き方はコチラです あ、ちなみに分配法則などで 「()を外すこと」を「式を展開 分配法則のコツは、かけ算の処理を 「符号→数字→文字」 の順番で行うことです。 計算問題は、正確かつ高速に解いてナンボなので、確実にマスターしましょう。 そのためには何回も解く必要が出てくるかもしれませんよね？ ご安心ください。
3
分配法則の練習問題5灘中学入試 分配法則に関するまとめ 分配法則とは まずは分配法則を、かんたんにおさらいしておきます。 (分配法則) a × ( b c) = a × b a × c a × ( b c) = a × b a × c ( a b) × c = a × c b × c ( a b) × c = a × c b × c 絵で表すとこんな感じです。 ※ a × b a × b のことを a b a b と表記していますが、中学数学から「×」の記号を省略することが 分配法則、交換法則、結合法則の問題 3つの法則を整理しておきます。 文字を使って書きますが、次の通りになります： 分配法則：$a \times (bc) = a \times b a \times c$ 交換法則：$a b = b a$ もしくは $a \times b = b \times a$ 結合法則：$(a b) c = a (bc)$ もしくは $(a \times b) \times c = a \times (b \times c)$ です。分配法則の利用 基礎 例題1 12×(1 63 4) = 12× 1 6 12× 3 4 = 29 =7 このような場合、カッコ内を計算せず、分配法則でカッコを開いたほうが計算が簡単になる。 次の計算をせよ。 ×(1 2 3 4) (1 31 7)×21 36×(2 95 4) (7 121 8)×(24) 例題2
分配法則の復習 基本正負の数と分配法則でも見た通り、分配法則とは、次のような計算ができることを言います。 \begin{eqnarray} \bigcirc\times(\square\triangle) &=& \bigcirc\times\square\bigcirc\times\triangle \\5pt (\square\triangle)\times\bigcirc &=& \square\times\bigcirc\triangle\times\bigcirc \\5pt \end{eqnarray} 、 、 には 数学・算数 代数の問題です 代数の問題です 可換環R上の全行列環Mn(R)の乗法モノイドに関する単元群について GLn(R)＝Mn(R)^×＝｛A∈Mn(R) ｜detA∈R^×｝となることを 質 1分配法則 分配法則とは 数の加法と乗法について次の式が成り立つ事 例1) を計算せよ。 例2) を計算せよ。 例3) を計算せよ。
19年05月23日 小学校算数。 公式と交換法則・分配法則。 問題 底辺7㎝、高さ13㎝の平行四辺形の面積を求めなさい。 四角形の面積は、5年生で学習します。 平行四辺形の面積の公式は、底辺×高さ＝面積 です。 7×13＝91 答え 91c㎡ となります。 しかし分配法則は何に役立つのか？ 分配法則が頻繁に使われるのは中学校数学からですが、小学校算数でも知っていたら活用できる機会はありますし、生活の中でも使うことができます。 特に分配法則の逆 \(a×ba×c=a×（bc）\) というテクニックは頻出です。カッコをひらいて計算する かっこを開く方法 を 分配法則 という。 かっこのある式では普通かっこ内を先に計算するが、分配法則でかっこを開いてから計算したほうが計算しやすい場合もある。 a × (b c) = a×b a×c aをかっこの中のb,cそれぞれにかける (例) 18× ( 4 9 − 5 6 ) このような問題ではカッコの中の分数の計算をするより分配法則でカッコを開いたほうが
分配法則を中学受験の問題で使いこなそう 小学生がつまずきやすい逆や分数 遊ぶ数学
分配法則を中学受験の問題で使いこなそう 小学生がつまずきやすい逆や分数 遊ぶ数学
関数 (動点) 中1数学 点の動きを処理する問題で最初は戸惑うかもしれませんが、パターンが決まっているので慣れると決して難しくはありません。 動点は2年生、3年生になっても出てきますので今のうちに定着させましょう。 たくさん練習して練習 分配法則を使った因数分解 (変数なし) これは現在選択されている項目です。 GCF (最大公約数) と LCM (最小公倍数) の文章問題 1 中学数学 問題「分配法則」の問題の入試問題、厳選9問（基礎からのやり直し、苦手克服、復習ドリル）計算 問題集 11 高校入試問題（過去問）：分配法則の計算編 12 (1), 6 a × ( − 3) （埼玉県） 13 (2), 1 2 ( 6 a 4) （三重県） 14 (3), 2 ( a − 3 b) 3 ( a b) （栃木県） 15 (4), − 3 ( x 2) ( 7 − 9 x) （佐賀県） 16 (5), ( 2 x 1) − 3 ( 1 − x) （沖縄県） 17 (6
分配の法則 符号ミスがなくなる決定版 中学数学の無料オンライン学習サイトchu Su
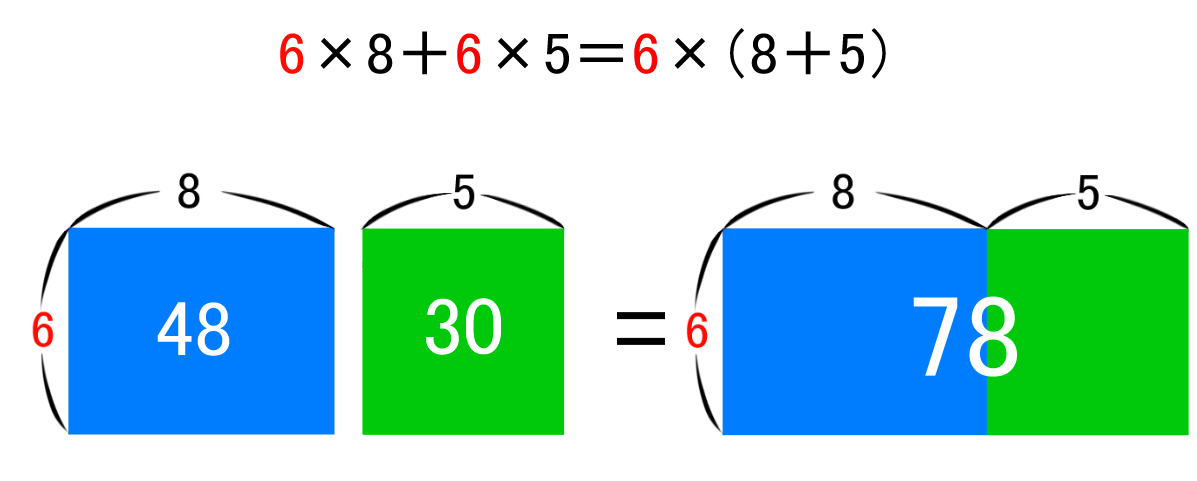
正負の数 6 工夫して計算する 分配法則など バカでもわかる 中学数学
分配法則を実際に使ってみよう！ それでは、この問題に分配法則を使ってみましょう。 2つの項があります。 さらに、この2つの項には、 「43」という同じ数がかかっている ということに注目してください。 なので、この式に分配法則を使うことが出来ます！分配法則を使って、かけ算の「10×」をカッコの中に分けて配ると分数が消えてくれる よ。 ①の答え ②もカッコの中の分数のたし算が面倒くさそうだね。中学3年生 数学 平方根の加法・減法 問題プリント 無料ダウンロード・印刷 √の中が等しい数は、文字式の同類項と同じように分配法則を使ってまとめることができることなどについて理解し、平方根の加法・減法を練習する問題プリントです。
小学生でも理解できる 分配法則 の教え方 活用できる問題例を紹介 数学fun
中学数学 正負の数 でつまずく原因と解決法 四則混合 分配法則
上記の問題を分配法則を使って解こうとすると、以下のようになります。 ①36× (－98)＝36× (－100＋2)＝36× (－100)＋36×2＝－3600＋72＝－3528 ※分配法則を使うために、無理やり (－98)を (－100＋2)の形にしている。分配法則を用いて、 1 1 次式の加減を計算します。 符号がどうなるのか、迷ってしまう人が出やすい単元です。 まずは意味を考えることより、計算ができることが大事です。 計算ルールを覚えて、機械的に処理できるようになることを優先しましょう。分配法則の仕組み 分配法則の仕組みを説明する上で一番わかりやすい例が長方形の面積です。 長方形の面積は『縦×横』ですが、1辺の長さが等しい2つの長方形の面積の合計を考えたら分配法則が視覚的に理解できます。 たとえば以下の問題。
分配法則とかっこの外し方 かっこの前がマイナスのときはミスりやすい 中学や高校の数学の計算問題
中1数学 文字の式 分配法則を使う計算 3つのパターン たけのこ塾 勉強が苦手な中学生のやる気をのばす
数学 分配法則 (ab)(cd)=という問題で、それぞれにかけると acadbcbdになりますよね？ これは公式なのでしょうか？ それともどうしてこうなるのか証明？というか説明できるので 質問No 数学Ⅰの問題で A=2x＋y＋z, B=x＋2y＋z, C=x＋y＋2z のとき、2A－3｛A－（B＋C）｝を計算せよ。 という問題の、中カッコのはずし方がイマイチ分かりません。－3は、中カッコの中の計 算ができたら分配法則するのでしょうか？分配法則 1 分配法則でかっこをひらきなさい。 2(3x1) 4(2x7)5(2a3b)7(2p1) 2 分配法則でかっこをひらきなさい。 1 2 (4x12) 3 5 (10x1)2 3 (9a12b)3 8 (12c16 3) 3 分配法則でかっこをひらきなさい。 (12x9)÷3 (8y24)÷(4) (12a10b)÷(6) (36x8)÷(12) 4 分配法則でかっこをひらき
3
分配法則を見やすいイラストで慶應生が超丁寧に解説 証明 問題付き 高校生向け受験応援メディア 受験のミカタ
今回のテーマは「分配法則」と呼ばれる、すごく重要な計算だよ。 分配法則とは、かけ算を分けて配る法則 のこと。 例えば、分配法則は （10＋2）×3 のような式で使うんだ。 例 （10＋2）×3 これまでの計算ではカッコの中を優先したので、 （10＋2） ×3分配法則でかっこを開いてから同類項をまとめる。 2(3x4)4(2x6) = 6xx24 = (68)x4 = 14x32 5(2a1)3(a5) = 10a5 3a15 = (103)a515 = 13a10 4(5x2y)3(6x7y) = x8y18x21y = (18)x(1)y = 38x13y 9(x3)6(2x4) = 9x2712x24 = (912)x2724 = 3x51 2(3x1)5(x8) = 6x25x40 = (65)x240 今日の授業ノートです 学年 中学1年生, キーワード 中1,分配法則,数学,math
中1数学 分配法則の逆 練習編 映像授業のtry It トライイット
中学生レベルの数学の質問です 画像のとうり 分配法則と乗法公式 Yahoo 知恵袋
数学の平均変化率の問題がわかりません 374の の途中式な Yahoo 知恵袋
文字式の計算 カッコ 分数を含む多項式 計算ドリル 問題集 数学fun
文字式の 分配法則 の公式が成り立つ仕組みを解説 数学fun
Studydoctor分配法則による多項式の展開 中３数学 Studydoctor
中１数学 正負の数 分配法則 オンライン無料塾 ターンナップ Youtube
数学 中1 無料学習プリント教材
中３数学 平方根 ２６ 中学数学高校数学個別指導in山形市 数専ゼミ
中1数学 分配法則 練習編 映像授業のtry It トライイット
一次式と数の乗除 文字式と数の分配法則のルールを覚えよう 中学や高校の数学の計算問題
問一は二次方程式の問題と 数学的帰納法を用いてビネの公式が成り立つことを示せとなって Clear
世界一わかりやすい数学問題集中２ 1章 式の計算
中学３年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ
高校数学 3つの集合の共通部分 和集合 補集合 結合法則と分配法則 ド モルガンの法則の拡張 ベン図 受験の月
分配法則とは 証明や分数 割り算を含む計算問題 小学生の復習 受験辞典
中３数学 平方根 ２９ 中学数学高校数学個別指導in山形市 数専ゼミ
中学生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
たけのこ塾 V Twitter 中1数学 分配法則 の問題の画像をアップしました 分配法則 分配法則の逆 解答 解説
数学が苦手なら必見 再掲 意外と忘れている数学の超基本
無料 中１数学 基本解説 問題プリント 正の数 負の数11 四則計算 111
3分で分かる 分配法則の仕組みとやり方をわかりやすく 合格サプリ
中学３年生 数学 平方根の加法 減法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
分配法則
中学受験算数 分配法則の逆を使った問題 Stupedia
正負の数 6 工夫して計算する 分配法則など バカでもわかる 中学数学
無料 中１数学 基本解説 解答プリント 方程式３ 解き方２ 124
中１数学 正負の数 ５５ 1 中学数学高校数学個別指導in山形市 数専ゼミ
中学数学分数この問題は分配法則を使えるんですか 使えるのであれば分配法 Yahoo 知恵袋
中1数学 分配法則 練習編 映像授業のtry It トライイット
数学 中1 無料学習プリント教材
乗法公式 無料で使える中学学習プリント
1
小学生でも理解できる 分配法則 の教え方 活用できる問題例を紹介 数学fun
3つの法則 交換法則 結合法則 分配法則 さわやか さくらぐみ
分配法則を中学受験の問題で使いこなそう 小学生がつまずきやすい逆や分数 遊ぶ数学
正負の数 中1で学習する分配法則問題ののやり方とは 中学数学をはじめから分かりやすく
分配法則を中学受験の問題で使いこなそう 小学生がつまずきやすい逆や分数 遊ぶ数学
分配法則の問題 小学生から中学生まで幅広く使う公式だ 中学や高校の数学の計算問題
無料 中１数学 テスト対策問題 問題プリント 107 正の数 負の数７ 利用
数学について 難しいです これを展開をして下さい ただし 分配法 Yahoo 知恵袋
たけのこ塾 V Twitter 中1数学 分配法則 の問題の画像をアップしました 分配法則 分配法則の逆 解答 解説は画像をご覧下さい 勉強垢 数学 正負の数 中1
分配の法則 符号ミスがなくなる決定版 中学数学の無料オンライン学習サイトchu Su
文字式 １次式 の計算 無料で使える中学学習プリント
3分で分かる 分配法則の仕組みとやり方をわかりやすく 合格サプリ
分配法則を見やすいイラストで慶應生が超丁寧に解説 証明 問題付き 高校生向け受験応援メディア 受験のミカタ
たけのこ塾 No Twitter 中1数学 文字式 いろいろな計算 についての問題を作成しました 今回の問題 をすべて解くことができれば 文字式の計算問題は大丈夫です 分配法則を使って 計算を行っていきましょう 勉強垢 中1 数学 文字式
無料 中１数学 基本問題 問題プリント 正の数 負の数11 四則計算 111
中学生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
中1数学 分配法則 練習編 映像授業のtry It トライイット
数学 中1 無料学習プリント教材
中学数学 問題 6 分配法則の計算 の入試過去問 厳選９問 基礎からのやり直し 苦手克服 復習ドリル 計算 問題集 行間 ぎょうのあいだ 先生
数学 中１ 正負の数の 分配法則 の計算練習 入門 基礎問題37 正負の数 Youtube
小学生でも理解できる 分配法則 の教え方 活用できる問題例を紹介 数学fun
文字式の 分配法則 の公式が成り立つ仕組みを解説 数学fun
中学３年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
中学2年数学 式の計算 多項式と数の乗法 掛け算 除法 割り算 分配法則を使って計算しよう 数学の面白いこと 役に立つことをまとめたサイト
中1数学 分配法則の逆 練習編 映像授業のtry It トライイット
分配法則を使った文字式の展開 Youtube
中3数学 平方根 分配法則を利用する計算問題 Youtube
平方根の式を分配法則で計算する4つのステップ Qikeru 学びを楽しくわかりやすく
1 4 の問題なのですが 高校の数学の場合 分配法則で解くのはいいのでしょうか Clear
中1数学第1章1６分配法則 応用問題 Youtube
ベスト中2 数学 式の計算 問題 最高のぬりえ
4 1 式の計算 分配法則 勉強できようサイト
無料 中１数学 基本問題 解答プリント 文字の式１ 数量１ 113
分配法則 問題 Youtube
分配法則 1次式の計算 中学数学の無料オンライン学習サイトchu Su
無料 中１数学 標準問題 問題プリント 112 正の数 負の数12 四則計算２
彦根市の学習塾講師が紹介する中間テスト対策勉強法 中学１年生 乗法の交換結合分配法則 確認問題 彦根市の高校数学専門個別指導学習塾 安澤数学教室
分配法則を見やすいイラストで慶應生が超丁寧に解説 証明 問題付き 高校生向け受験応援メディア 受験のミカタ
中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ
分配法則とは 証明や分数 割り算を含む計算問題 小学生の復習 受験辞典
中1数学 03 8 分配法則 問題 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト
たけのこ塾 Twitterren 中1数学 今回も かっこのある方程式 についての問題を作成しました 最初に分配法則を用いて カッコを外してから計算しましょう 勉強垢 中1 数学 方程式
分配法則を見やすいイラストで慶應生が超丁寧に解説 証明 問題付き 高校生向け受験応援メディア 受験のミカタ
式の乗法 分配法則で展開する問題に慣れよう 中学や高校の数学の計算問題
たけのこ塾 No Twitter 中1数学 文字式 いろいろな計算 についての問題を作成しました 今回の問題 をすべて解くことができれば 文字式の計算問題は大丈夫です 分配法則を使って 計算を行っていきましょう 勉強垢 中1 数学 文字式
正負の数 6 工夫して計算する 分配法則など バカでもわかる 中学数学
中学数学 分配法則 英語で数学を学ぼう Unit2 5 Umiの休憩部屋
中１数学 正負の数 ５５ 2 中学数学高校数学個別指導in山形市 数専ゼミ
分配法則の問題 この公式さえ覚えていれば 展開できまくる 中学や高校の数学の計算問題
1
数学分配法則を使って解きなさい という問題なのですが と の途中式は分配法則 Yahoo 知恵袋
無料 中１数学 基本問題 解答プリント 正の数 負の数11 四則計算
4 1 式の計算 分配法則 勉強できようサイト
中1数学 正の数 負の数 分配法則とは何か たけのこ塾 勉強が苦手な中学生のやる気をのばす
Q Tbn And9gctxhg2kum45l2wdza1oumpudzubqeoqcte3tym06bhui43jfwcl Usqp Cau
4 1 式の計算 分配法則 勉強できようサイト
分配法則を見やすいイラストで慶應生が超丁寧に解説 証明 問題付き 高校生向け受験応援メディア 受験のミカタ
正負の数の計算ー四則混合 無料で使える中学学習プリント
文字式と分配法則 Youtube
小学生でも理解できる 分配法則 の教え方 活用できる問題例を紹介 数学fun
0 件のコメント:
コメントを投稿