これは、性質1で証明した結果を使えば簡単に証明できます。 さきほどと同様に平行四辺形に対角線 A C を引きます。 すると、三角形 A B C と C D A は合同でした。 よって、 ∠ B = ∠ D が分かります。それぞれ平行である四辺形をいう。 対角線とは向かい合う角を結ぶ線分をいう。 (以下、定義の補足(命題1ー34)(平行四辺形・対角線)という) 平行四辺形、対角線の用語は初めてここに登場する。 対辺、対角は、定義1ー22の補足による。 等しいは、公理平行四辺形になるための条件 四角形 \(abcd\) が平行四辺形であることを示せ。 このような問題を学習していきます。 四角形 \(abcd\) が平行四辺形であることを示すためには、 以下の \(5\) つのうち、ど
平行四辺形の3つの性質とその証明 具体例で学ぶ数学
平行四辺形 対角線 長さ 等しい 証明
平行四辺形 対角線 長さ 等しい 証明-2組の向かい合う角(対角)がそれぞれ等しい四角形は、平行四辺形である。 ④ 対角線が、それぞれの中点で交わる四角形は、平行四辺形である。 (3) ① (定義だから) 2 (解答例) ② 証明対角線ACをひく。 ABCと CDAにおいて 中学数学 図形 平行四辺形とは? 定義・条件・性質や面積の公式、証明問題 21年2月19日 この記事では、「平行四辺形」の定義や条件、性質をできるだけわかりやすく解説していきます。 また、平行四辺形の面積の公式や、対角線の角度などの計算問題



Www Tsumugi Ne Jp Member Data Sm2 5 Sm2 5 4 Pdf
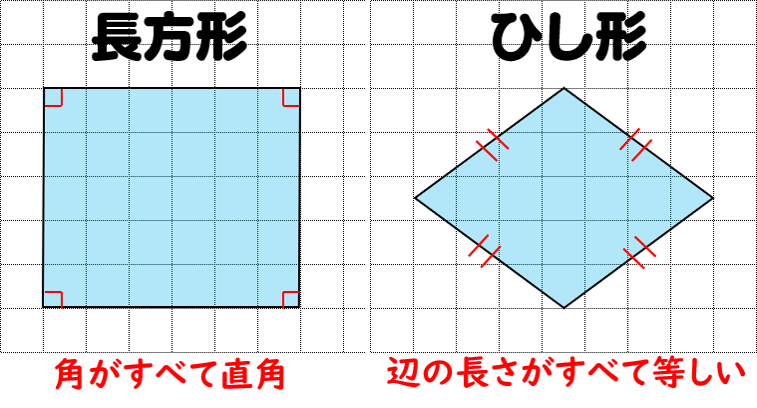
ひし形と正方形、平行四辺形との違い ひし形、正方形、平行四辺形の違いを下記に示します。 ひし形 ⇒ 全ての辺の長さが等しい四角形 平行四辺形 ⇒ 2組の辺の長さ等しい四角形 正方形 ⇒ 全ての辺の長さ・角度が等しい四角形 ひし形と対角線の関係2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ④ 4 四角形は,1組の向かい合う辺が平行でその長さが等しいとき,平行四辺形になります。∠a=∠cbe(平行線になる条件) AB//DC AD//BC <戻る> 4 対角線が、それぞれの中点で交わる。 ABOと CDOで AO=CO 1 BO=DO 2 対頂角)3 1,2,3より2辺とその間の角がそれぞれ等しいので
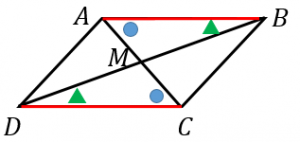
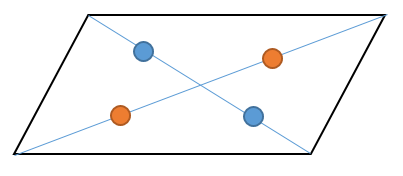
図のように対角線上にある角度の大きさが等しいと言えれば 平行四辺形であると証明出来ます。 ④2つの対角線がそれぞれの中点で交わる 図のように対角線を引いたとき、紫の点が赤の対角線、 オレンジの対角線の中点になれば平行四辺形だと証明出来平行四辺形は、点対称な図形である。対称の中心は、対角線の交点に等しい。 平行四辺形の対角線によって、平行四辺形を互いに合同な2つの三角形に分けることができる。 平行四辺形の面積sは 〔底辺〕×〔高さ〕 で求めることができる。平行四辺形の定義は、「\(\boldsymbol{2}\) 組の向かい合う辺が平行な四角形を平行四辺形という 」になります。また、平行四辺形になるためには、定義を含めて \(\boldsymbol{5}\) つの条件 があります。
上のまとめに示したように「平行四辺形」の定義は「2組の向かい合う辺がそれぞれ平行である四角形」すなわち「 ad//bc , ab//dc 」が成り立つ四角形なので,仮定や結論が「平行四辺形」になっているときは「 ad//bc , ab//dc 」に置き換えるとよい この頁では平行線の性質について,証明の進め方平行四辺形の性質と図形の証明 ワークシート 〔平行四辺形の性質〕 右の図で、四角形abcd は 平行四辺形である。 ec の長さを求めなさい。 問1 a b c e 4 ③ 2 組の対角がそれぞれ等しい ④ 2つの対角線が互いの中点で交わる 平行四辺形の定義↓ 2組の対辺がそれぞれ等しい。 2組の対角がそれぞれ等しい。 2組の対辺がそれぞれ平行。 2本の対角線がともに、互いの中点で交わる。 1組の対辺が平行であり、かつその長さが等しい。 です!



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



平行四辺形に対角線の長さが等しいという条件を足すと長方形になりますか な Yahoo 知恵袋
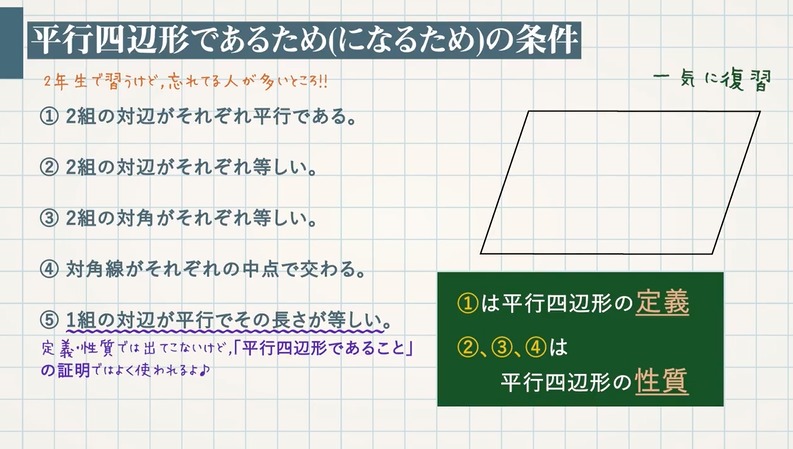
平方四辺形を対角線で分けた $4$ つの三角形の面積は等しいから、平行四辺形の面積は、 $4\times \dfrac{3\sqrt{3}}{2} = 6\sqrt{3}$ だね! まとめ 平行四辺形の面積を対角線の長さと角度から求めるのに必要な特徴は、③ $\textcolor{blue}{2}$ 組の対角がそれぞれ等しい。 ④ 対角線がそれぞれの中点で交わる ⑤ $\textcolor{blue}{1}$ 組の対辺が平行でその長さが等しい →定義・性質では出てこないけど、「平行四辺形であること」の証明ではよく使われます。 ①は平行四辺形の 定義/平行四辺形になる条件/平行四辺形になることの証明/ 対角線に注目/ 三角形の合同を先に証明/いろいろな四角形/面積が等しい三角形/ 面積を求める /等積変形/FdData 中間期末製品版のご



中点連結定理を使った平行四辺形であることの証明 教遊者




平行四辺形の面積の求め方 公式と計算例
平行四辺形と長方形、正方形との関係 長方形、正方形は、「特別な平行四辺形」です。長方形は、平行四辺形の性質を満たし、加えて ・2本の対角線の長さが等しい という性質を持ちます。 正方形は、平行四辺形の性質に加えて ・対角線の長さが等しい ただの位置関係しか示せなかった同位角が、証明のエースに化ける魔法の言葉です。 l と m は平行な直線です。 この場合、∠ a と∠ b の角の大きさは等しくなります。 そのことを平行線の同位角は等しいので、∠ a =∠ b と書きます。(3) 平行四辺形の性質は,上で証明したことの他にもまだいくつかあります。平行四辺形の性質と して正しいものを下のアからオの中から1つ選びなさい。 ウ 対角線が垂直に交わっている。 エ 対角線の長さが等しい。 オ AB=BC,AD=DCである。




正方形の数 公式 正方形の面積を求める公式は 正方形の面積 一辺 一



中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく
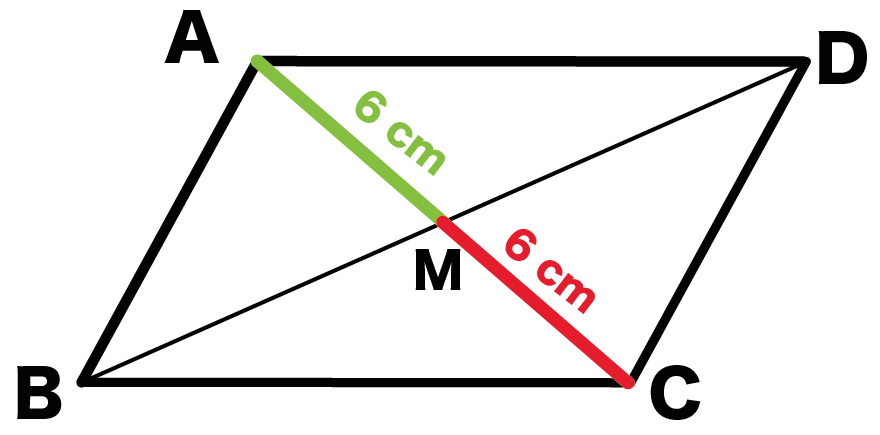
平行四辺形では、対角線を引くと それぞれの中点で交わります。 厳選6パターンの問題に挑戦! それでは、平行四辺形の角度、辺の長さを求める問題をパターン別に解説していきます。 対角、対辺の基 31 平行四辺形の性質その1:対辺の長さが等しい 32 平行四辺形の性質その2:対角の大きさが等しい 33 平行四辺形の性質その3:対角線が他の対角線の中点を通る 4 平行四辺形の面積 (公式・証明) 5 平行四辺形の成立条件 51 平行四辺形の成立条件その1:2 2) 平行四辺形の対角線の交点をO、各頂点をABCDとする。 かなり省略して証明するが、∠AOB=∠BOC=∠COD=∠DOA=90° 平行四辺形の対角線はそれぞれの中点で交わる。 よって、対角線で区切られた4つの三角形は全て合同。 故に、4つの三角形全ての斜辺は等しい。



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー




平行四辺形の対角線の長さの求め方
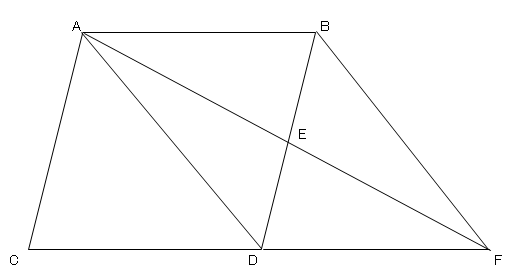
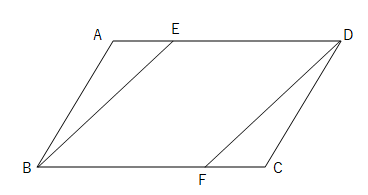
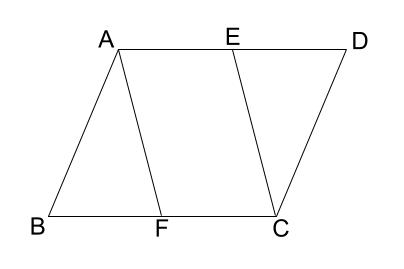
三角形の合同の証明の利用 四角形 \(abcd\) が平行四辺形であることを示すために、 辺の長さ、角の大きさが等しいことを示したいときがあります。 これを示すために、 「三角形の合同を証明し、そこから示す」 ということ平行四辺形になると思うよ。 僕がかいた図でも,平行四辺形にみえるよ。 四角形EBFDはどんな四角形になりそうですか。図をかいてみましょう。 「四角形EBFDは平行四辺形になる」という結論を示すために,何がわかればよいですか。ひし形の定理 定理 ひし形の2組の向かい合う角の大きさはそれぞれ等しい。 定理 ひし形の対角線はそれぞれ中点で垂直に交わる。 定理 対角線がそれぞれ中点で垂直に交わる四角形はひし形である。 定理 隣り合う2辺の長さが等しい平行四辺形は 定 菱形(ひしがた、りょうけい)、斜方形




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
対角線 ac と pq の q , r , s とおくとき,四角形 pqrs はつねに平行四辺形になることを証明 ※ この問題では「向かい合う1組の辺が平行でかつ長さが等しい → 平行四辺形」という定理を使ったが,「2組の向かい合う辺がそれぞれ平行 → 平行四辺形」と1 組の対辺が平行でその長さが等しいから,四角形efgh は平行四辺形である。 4.振り返り(Ⅰ) 「今回の証明ではどこに補助線を引いて証明を進めたかな?対角線 四角形の、向かい合う頂点同士をむすんだ直線のことを、対角線といいます。 ・2本の対角線が、それぞれのまん中の点で交わる四角形平行四辺形、ひし形、長方形、正方形 ・2本の対角線の長さが等しい四角形長方形、正方形




等脚台形の定義と性質 中学校数学の範囲内で考える 身勝手な主張




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
平行四辺形において 1.対角線の長さが等しいなら長方形である. 2.対角線が直交するならひし形である. 3.対角線の長さが等しく直交するなら正方形である. 証明 1. abdと bacにおいて 3辺がそれぞれ等しいから abd≡ bac ∠a=∠b さらに,こんにちは、ウチダです。 今日は、中学 $2$ 年生の内容である 「平行四辺形になるための $5$ つの条件」 について、平行四辺形の定義から性質を証明し、そのあとで性質と条件が具体的にどう違うのかを詳しく見ていきましょう。 平行四辺形の定義とは まず、「平行四辺形とは何か」口で説明 まとめ:長方形の対角線の長さはやっぱり等しい。 長方形の性質の、 対角線の長さはそれぞれ等しい はおさえておこう! 三角形の合同で簡単に証明できるから安心だね。 そん



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
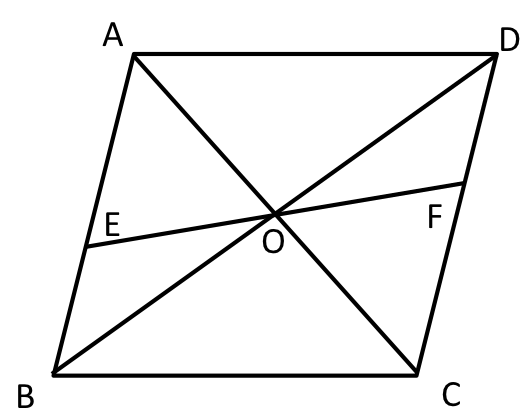



フロー 2 5 5 2 平行四辺形の性質を利用した証明
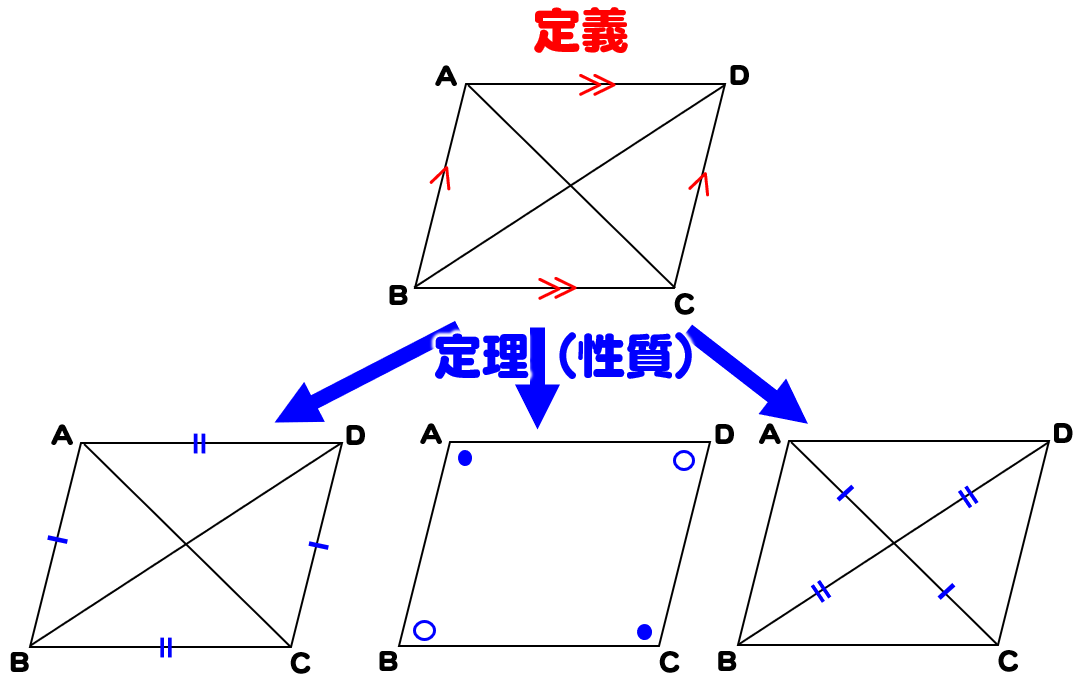
平行四辺形の定義と性質 定義 向かい合う2組の辺がそれぞれ平行な四角形 定理(性質) 2組の対辺がそれぞれ等しい 2組の対角がそれぞれ等しい 対角線がそれぞれの中点で交わる 定義は 「こういう四角形を平行四辺形としよう」 と決めたことなので 平行四辺形はたくさんの性質があります。 ①2組の対辺はそれぞれ等しい ②2組の対角はそれぞれ等しい ③対角線はそれぞれの中点で交わる 定理:1組の対辺が平行で、その長さが等しい たくさんありはしますが、平行四辺形とイメージするとでてくる対角線の長さが等しく、それぞれの中点で交わるとき長方形になる。 証明 それぞれの中点で交わるので四角形abcdは平行四辺形になる。 abcと dcbで 平行四辺形abcdの性質より ab=dc 1 bc=cb(共通) 2 仮定(対角線の長さが等しい)より ac=db 3



1




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット
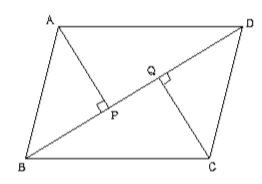



中2数学 平行四辺形の証明のポイントと練習問題 Examee




無料 中2数学 標準問題 解答プリント 232 平行四辺形3 長方形とひし形
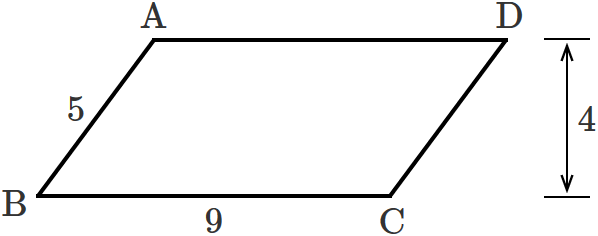



平行四辺形の対角線の長さの求め方




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




と を解説つきで教えてください Clear




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学



3




平行四辺形の定義と性質 証明問題の解き方 数学fun



Math 平行四辺形 平行四辺形になることの証明 働きアリ The 2nd




算数 小4 19 四角形の特ちょう Youtube




長方形の性質 対角線の長さはなぜ等しいのか Qikeru 学びを楽しくわかりやすく
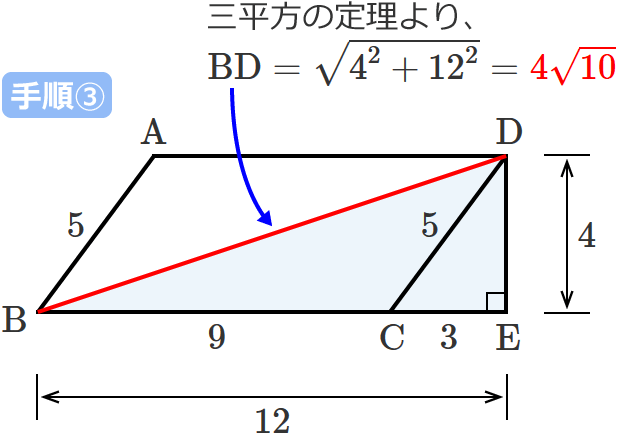



平行四辺形の対角線の長さの求め方



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




至急 1問でもいいので教えて下さい よろしくお願いします Clear
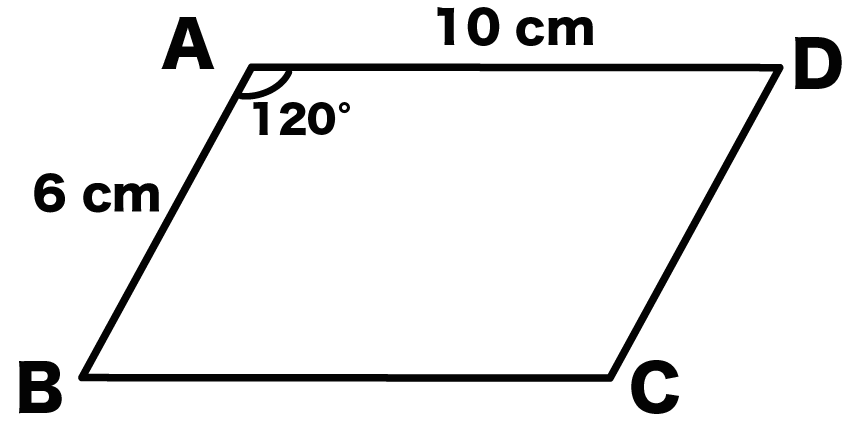



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
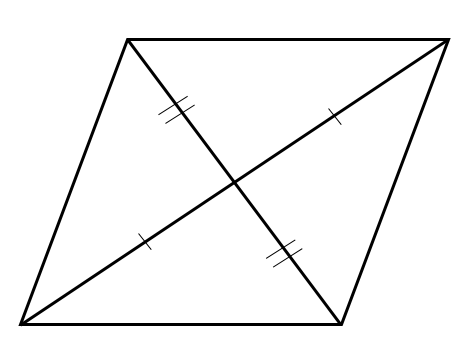



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
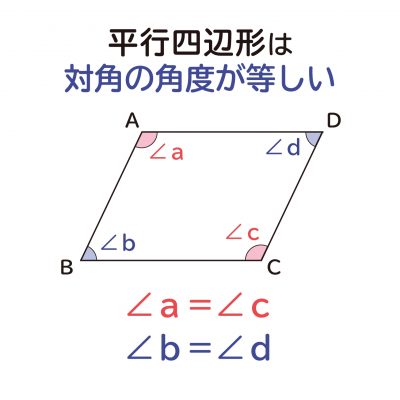



平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル



平面図形の基礎




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
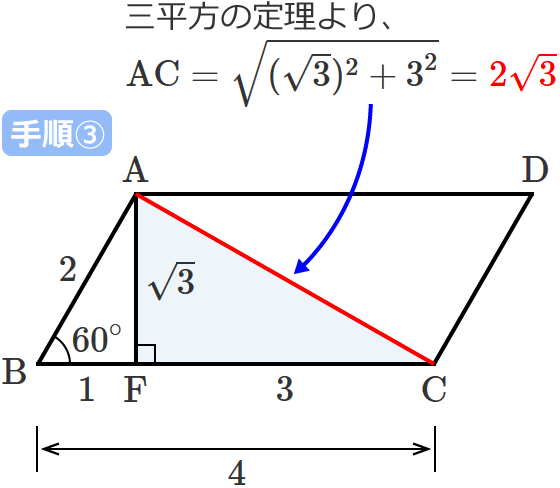



平行四辺形の対角線の長さの求め方




平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方




高校数学b ベクトルの成分表示と平行四辺形 受験の月
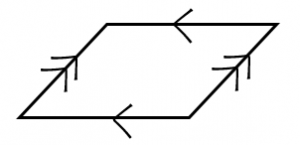



平行四辺形の3つの性質とその証明 具体例で学ぶ数学




中学数学 特別な平行四辺形について Clear




平行四辺形の3つの性質とその証明 具体例で学ぶ数学




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生



平行四辺形の二つの対角線の長さが違う理由って何ですか Aklv721 Yahoo 知恵袋




平行四辺形の性質 長さ 角度の問題 無料で使える中学学習プリント



平行 四辺 形 証明 平行四辺形になる条件の証明



Happylilac Net 4nen Sikakukei Ans Pdf
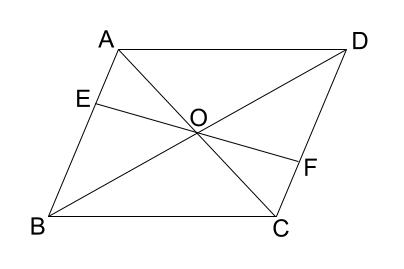



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su
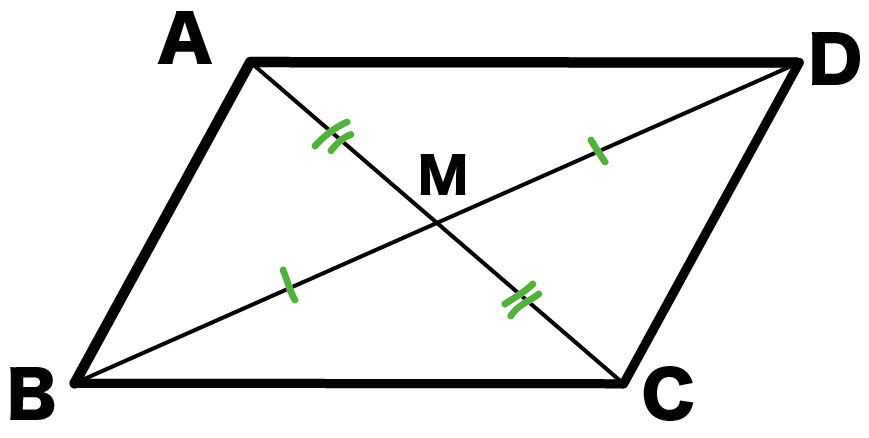



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学
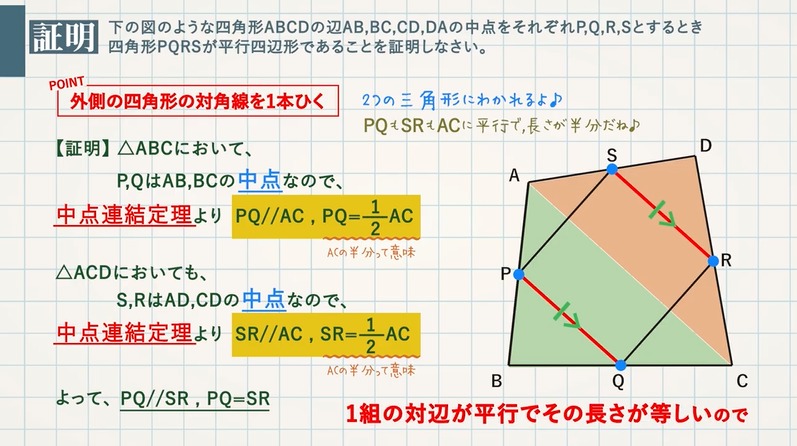



中点連結定理を使った平行四辺形であることの証明 教遊者



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



平行四辺形の性質の証明




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



中学数学 平行四辺形の証明問題を徹底解説 数スタ



対角線の長さが等しい平行四辺形は長方形である 対角線が垂 Yahoo 知恵袋



1



フロー 2 5 5 2 平行四辺形の性質を利用した証明



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係




無料 中2数学 テスト対策 解答プリント 216 図形と合同4 平行四辺形




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



Www Tsumugi Ne Jp Member Data Sm2 5 Sm2 5 4 Pdf



平行四辺形の証明 2 ネット塾



Www Tsumugi Ne Jp Member Data Sm2 5 Sm2 5 4 Pdf



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
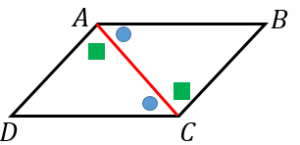



平行四辺形の3つの性質とその証明 具体例で学ぶ数学
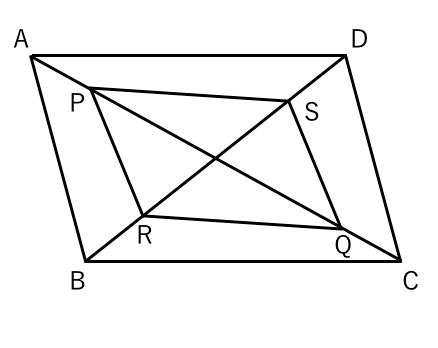



平行四辺形であることを証明する 苦手な数学を簡単に
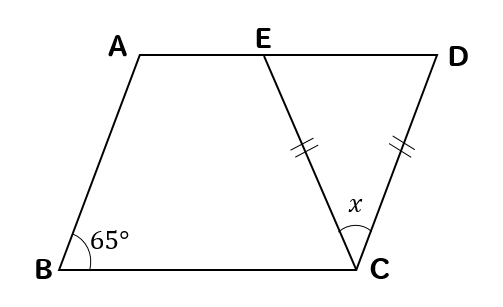



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
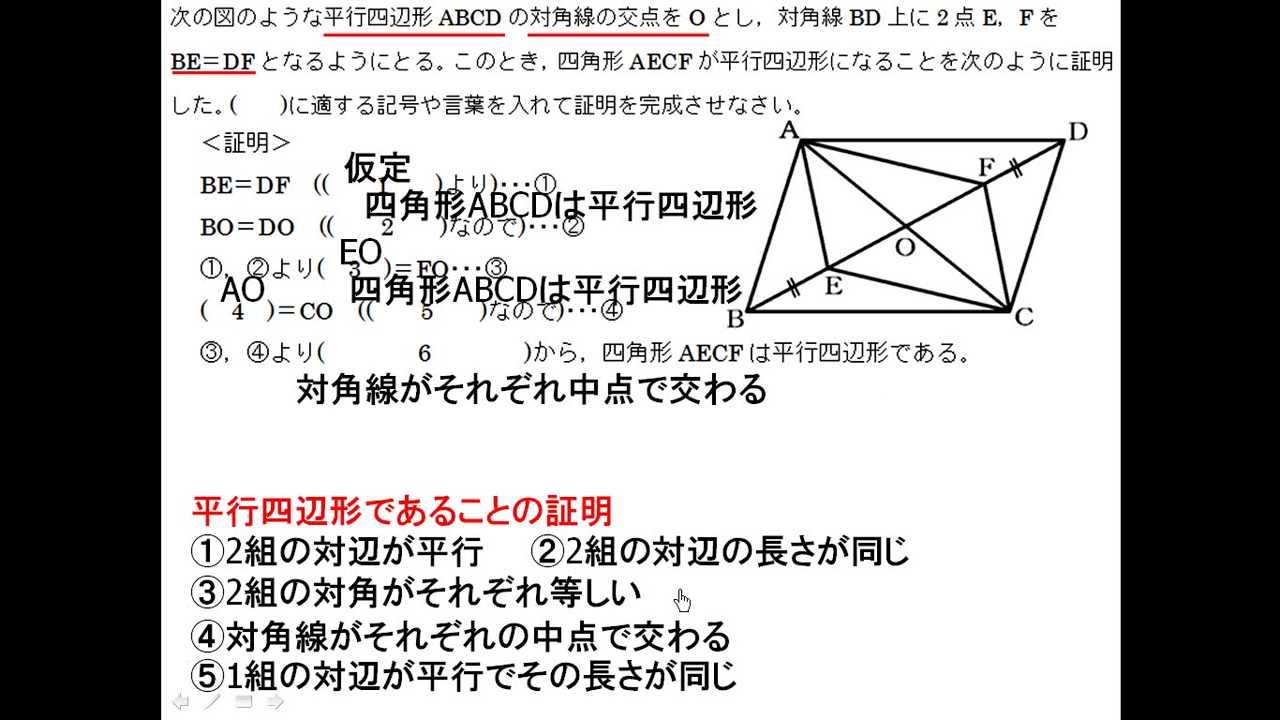



中2 数学 5 3 平行四辺形の証明 Youtube



中2数学 平行四辺形の証明のポイントと練習問題 Examee



1
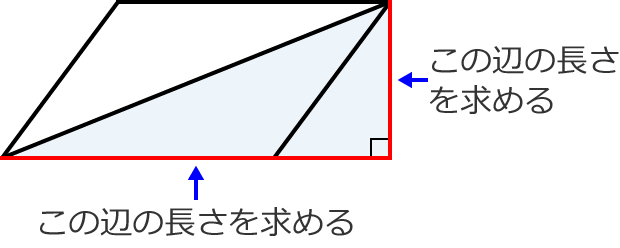



平行四辺形の対角線の長さの求め方



平面図形の基礎
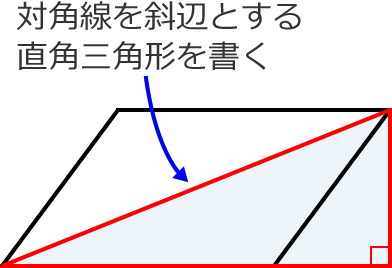



平行四辺形の対角線の長さの求め方




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット



平行 四辺 形 証明 平行四辺形になる条件の証明




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル




平行四辺形で知っておくべきこと 苦手な数学を簡単に




平行四辺形の対角線の長さの求め方




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室




2問とも分かりません 教えて下さい Clear
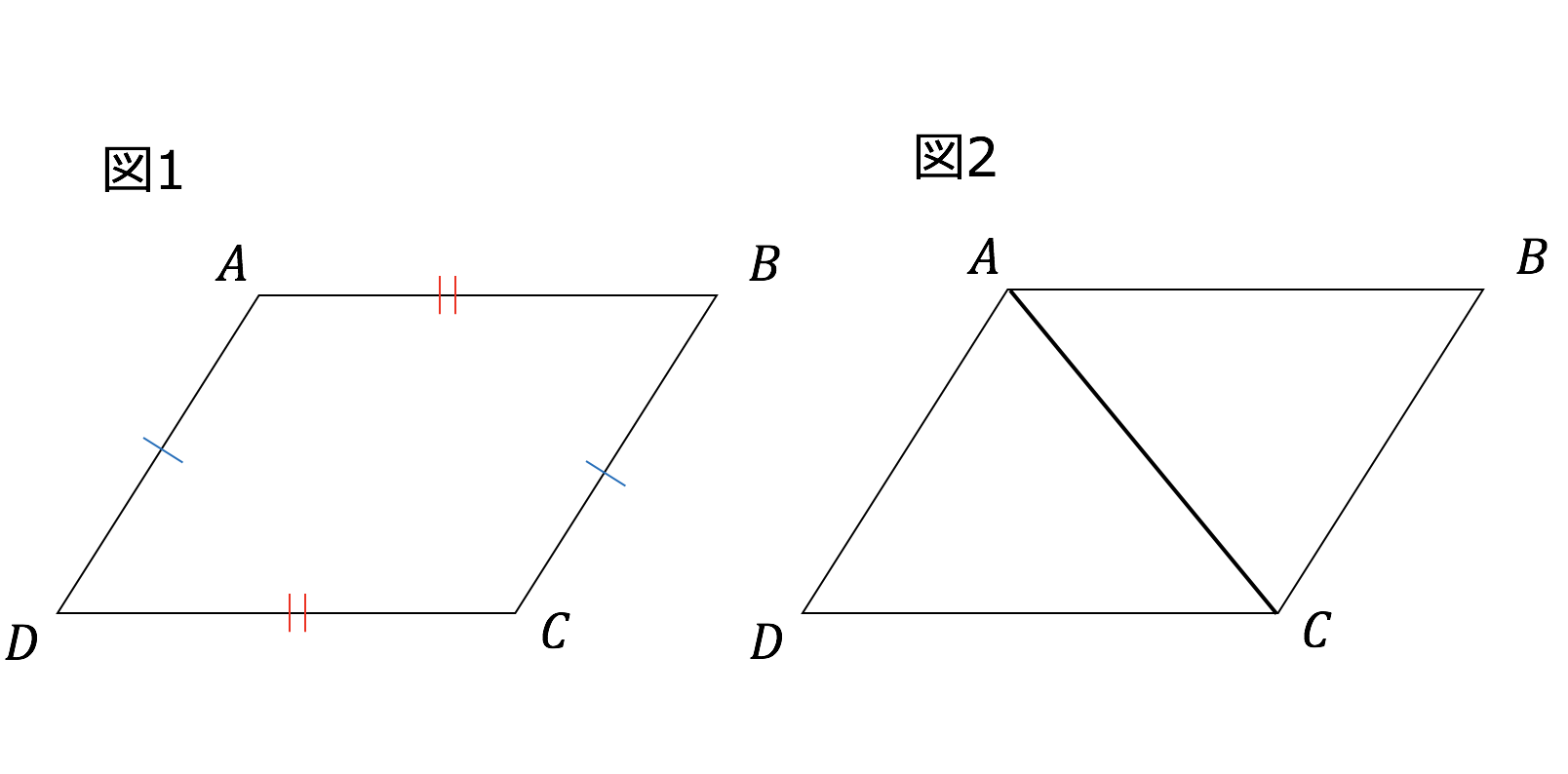



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ



高校入試 英語 数学 学習 三角形と四角形 平行四辺形




これ 問題の中に1つも平行ってワードがないのに どうして中点連結定理になるのか そし Clear




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




証明分かりません 教えてください Clear
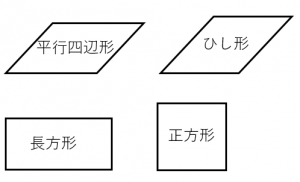



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学
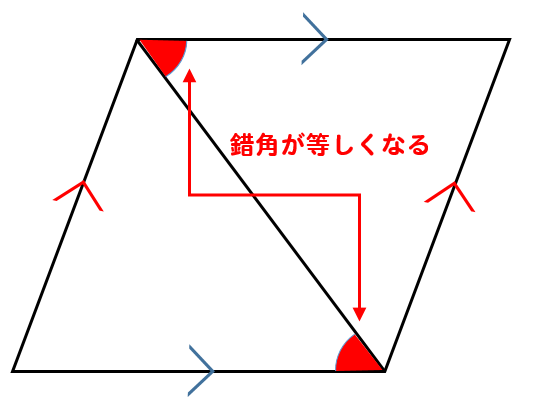



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




Math 平行四辺形 平行四辺形になることの証明 働きアリ
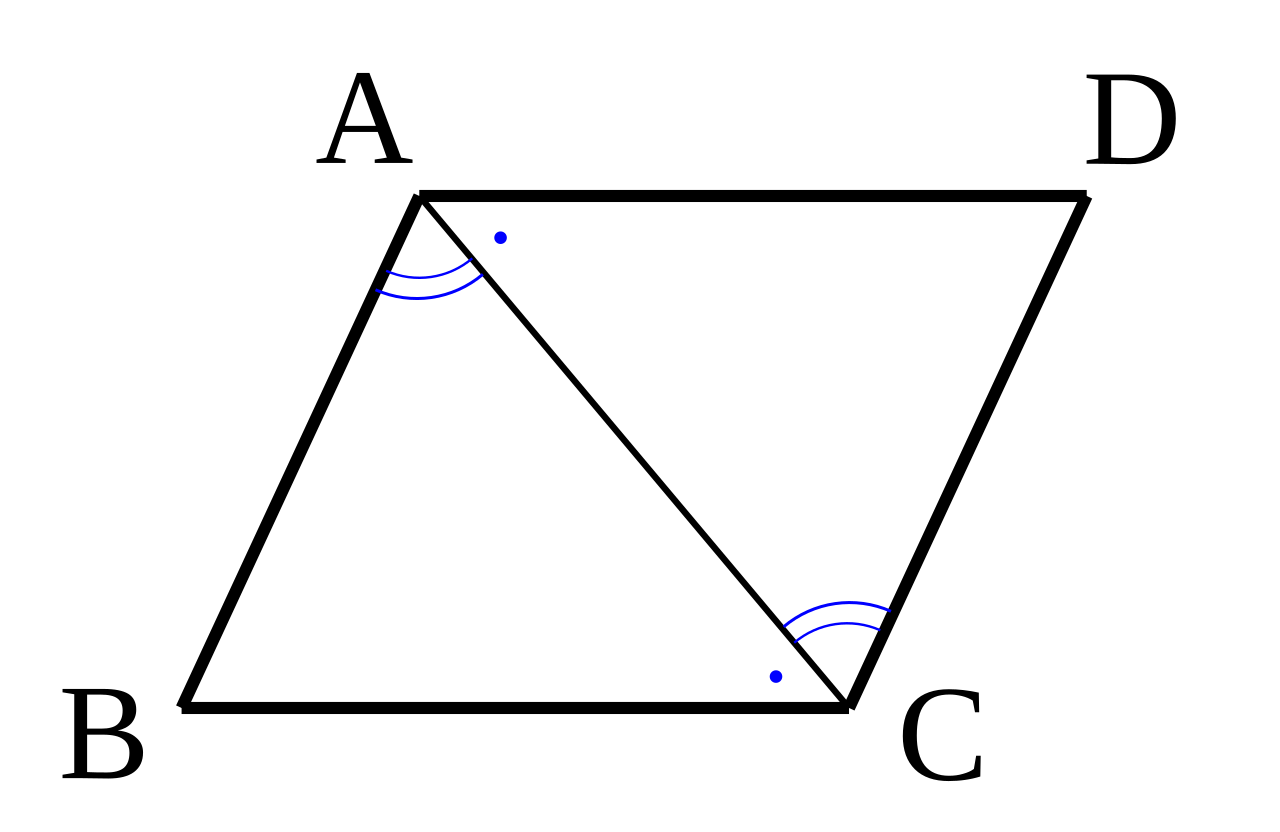



平行 四辺 形 証明 平行四辺形になる条件の証明




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
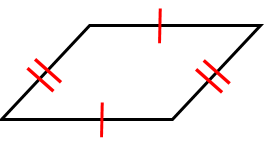



平行四辺形の3つの性質とその証明 具体例で学ぶ数学



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



平行四辺形の定義と性質 証明問題の解き方 数学fun



0 件のコメント:
コメントを投稿